Statistiek handleiding

Onderzoek is een essentieel onderdeel van je afstudeerscriptie. Bij veel onderzoeken geldt dat er ook een groot deel statistiek bij komt kijken. Omdat voor veel studenten statistiek toch een lastig onderdeel is, heeft Scriptie.nl een duidelijke handleiding opgesteld voor het opzetten en uitvoeren van statistisch onderzoek. Ook bieden wij een SPSS- en een onderzoekskunde-handleiding aan, deze kun je vinden onder het onderdeel scriptiehulp.

De statistiek manual is een initiatief van een aantal studenten met verschillende academische achtergronden, zowel technische als economische. Zij hebben geprobeerd om alle noodzakelijke kennis samen te vatten en in gebruikelijke taal uiteen te zetten. De schrijvers van deze handleiding gaan er van uit dat de lezers al enige voorkennis hebben van de basisbeginselen van de statistiek.

1. Basisbegrippen van de Statistiek

Deze bundel is een initiatief van verscheidene studenten met verschillende academische achtergronden, zowel technische als economische. Zij hebben getracht in een bundel alle noodzakelijke kennis samen te vatten en in gebruikelijk taal uiteen te zetten. De schrijvers gaan er van uit dat lezers van deze bundel enige voorkennis hebben van de basisbeginselen van de Statistiek. Studenten die onderzoek doen en de basis van de Statistiek al onder de knie hebben, kunnen direct doorbladeren naar hoofdstuk 11.

Veel plezier in de wereld van statistiek!

Arnoud Hattink

1.1 Introductie

Statistiek is een manier om informatie te verkrijgen van data.

Niets meer, niets minder. Veel studenten vragen zich af waarom statistiek boeken zo schrikbarend dik zijn als statistiek zich louter bezighoudt met het verkrijgen van informatie over data. Dit komt doordat studenten vandaag de dag geconfronteerd worden met verschillende soorten data die onderzocht kunnen worden met verscheidene methoden.

Om de beginselen van de statistiek te begrijpen is kennis van een aantal basisbegrippen en symbolen een noodzaak. In de tabel hieronder is een aantal symbolen met hun betekenis te vinden.

Α ∪ Β	De vereniging van gebeurtenissen Α en Β die plaatsvindt als Α of Β of beiden plaatsvinden
Α ∩ Β	De doorsnede van de gebeurtenissen Α en Β die plaatsvindt als Α en Β beiden plaatsvinden
Αc	Het complement van gebeurtenis Α vindt plaats als Α niet plaatsvindt
Α − Β	Het verschil tussen Α en Β
Α ⊂ Β	Α is een deelverzameling van Β

Een Venndiagram is een diagram dat gebruikt wordt om relaties tussen verzamelingen aan te geven. Het Venndiagram hieronder geeft een versimpelde illustratie van Α als deelverzameling van Β.

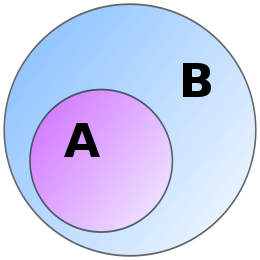
Figuur 1a. Α ⊂ Β (Bron: Wikipedia.nl)

1.2 Kansrekening

Als er een willekeurig experiment (ook wel random experiment=een actie of proces dat leidt tot een of meerdere mogelijke uitkomsten) wordt uitgevoerd zijn een paar begrippen van belang.

Alle mogelijke uitkomsten van zo'n experiment bij elkaar noemt men de uitkomstenruimte (Ω). Het complement van Ω noteert men als ∅ (=Ωc). Elk element van Ω heeft een uitkomst ω. De notatie ω ∈ Ω staat voor ″ω is element van Ω en deelverzamelingen van Ω heten gebeurtenissen.

Een paar (Ρ, Ω) dat bestaat uit verzamelingen Ω en kansfunctie Ρ noemt men een kansruimte. Deze kansruimte voegt aan elke deelverzameling Α ⊂ Ω een reëel getal op het interval [0;1] toe en wel op zo'n manier dat er sprake is van de twee volgende axioma's (axioma=een niet bewezen , maar als grondslag aanvaarde stelling):

1. Ρ(Ω)=1
2. als de deelverzameling A₁, A₂,... van Ω paarsgewijs disjunct zijn.

De kans op gebeurtenis Α noteert met als Ρ(Α). De term disjunct vereist wat toelichting. Twee gebeurtenissen Α en Β zijn disjunct als geldt Α ∩ Β=∅. Met andere woorden, Α en Β sluiten elkaar uit.

Uit de 2 bovenstaande axioma's kan het volgende geconcludeerd worden:

Als Α ⊂ Β dan Ρ(Β − Α)=Ρ(Β) − Ρ(Α)=Ρ(Αc ∩ Β)

Als Ρ(Αc)=1 − Ρ(Α); in geval van Α=Ω : Ρ(∅)=0

Als Α ⊂ Β dan Ρ(Α) ≤ Ρ(Β)

;dit is ook wel de ongelijkheid van Bonferroni

Als Α1, Α2, ..., Αn paarsgewijs disjunct zijn dan geldt Ρ(Α1 ∪ ... ∪ Αn =Ρ(Α1 + ... + Ρ(Α1)

Er is een uitzondering op al het bovenstaande: Heeft Ω een eindig aantal elementen (Ν) met allen gelijke kansen dan geldt Ρ(ω)=1 ⁄ Ν voor iedere &omega ∈ Ω. Tevens geldt dat is het aantal elementen van Α

Voorwaardelijke kans

Vaak wil men weten hoe twee gebeurtenissen gerelateerd zijn. Sterker nog, men wil de kans weten van een gebeurtenis gegeven dat een andere, gerelateerde gebeurtenis plaatsvindt. Deze kans noemt men de voorwaardelijke kans wordt als volgt genoteerd:

De kans op Α, gegeven Β is:

Ρ(Α | Β)=Ρ(Α ∩ Β) ⁄ Ρ(Β)

De kans op Β, gegeven Α is:

Ρ(Β | Α)=Ρ(Α ∩ Β) ⁄ Ρ(Α)

Voortbordurend op deze definities kan men de productregel toepassen:

Ρ(Α ∩ Β)=Ρ(Β) x Ρ(Α | Β)=Ρ(Α) x Ρ(Β | Α)

Voorbeeld 1c

Toptennisser Nedal speelt in de finale van het tennistoernooi Ronald Barros tegen de winnaar van de halve finale tussen Foderer en Kraaijenbek. Aangezien Kraaijenbek zijn beste jaren tennis al gehad heeft, schat men de kans dat Foderer de finale haalt op 86%. De kans dat Nedal Foderer in de finale verslaat is 67%, daar Nedal heer en meester is op gravel. De kans dat Nedal Kraaijenbek in de finale verslaat is nog groter, te weten 93%. De kans dat Nedal het toernooi wint, wordt dan als volgt berekend:

Ρ(Nedal wint Ronald Barros)=Ρ(Foderer wint halve finale) × Ρ(Nedal wint Ronald Barros | Foderer wint halve finale) + Ρ(Kraaijenbek wint halve finale) × Ρ(Nedal wint Ronald Barros | Kraaijenbek wint halve finale)

= 0,86 × 0,67 + 0,14 × 0,93=70,6 %

1.3 Onafhankelijke gebeurtenissen

Een van de doelen van het berekenen van de voorwaardelijke kans is het vaststellen of twee gebeurtenissen gerelateerd aan elkaar zijn of niet. Anders gezegd, men wil er achter komen of gebeurtenissen onafhankelijk zijn van elkaar.

Twee gebeurtenissen A en B zijn onafhankelijk van elkaar als:

Ρ(Α | Β)=Ρ(Α)

of

Ρ(Β | Α)=Ρ(Β)

Met andere woorden, twee gebeurtenissen zijn onafhankelijk van elkaar als de kans van een gebeurtenis niet beïnvloed wordt door het plaatsvinden van de andere gebeurtenis.

Voorbeeld 1d

Daan gooit 2 euromunten op. Beschouw de gebeurtenissen

Α: de eerste euromunt is kop
Β: de tweede euromunt is munt

De kans hierop is: Ρ(Α ∩ Β)=1⁄4=1⁄2 x 1⁄2=Ρ(Α) x Ρ(Β)

Gegeven de bovenstaande kans kan men concluderen dat α en β onafhankelijk zijn. Immers zal de uitkomst van de worp van de eerste euromunt geen invloed hebben op de uitkomst van de worp met de tweede euromunt (en andersom is uiteraard ook het geval).

1.4 De somregel

Met de somregel kan men de kans van de vereniging van twee gebeurtenissen berekenen. De kans dat gebeurtenis Α, of gebeurtenis Β, of beiden plaatsvinden is

Ρ(Α ∪ Β)=Ρ(Α) + Ρ(Β) − Ρ(Α ∩ Β)

De meeste studenten vragen zich nu per direct af waarom Ρ(Α ∩ Β) van Ρ(Α) en Ρ(Β) wordt afgetrokken. Dit komt doordat bij de optelling van Ρ(Α) en Ρ(Β) de kans Ρ(Α ∩ Β) dubbel wordt geteld en deze dient er weer vanaf getrokken te worden.

Voorbeeld 1 e

Arnold is bezig met zijn derde jaar Bachelor van Bedrijfskunde en heeft nog twee vakken openstaan die hij moet halen om in september aan zijn Master te beginnen. Aangezien Arnold erg druk is met zijn studie en daarnaast ook nog werkt, kan zijn werk invloed hebben op zijn studieresultaten. Zie 10 onderstaande tabel met de kansen dat hij wel of niet aan zijn Master begint gecombineerd met 1 of 2 dagen in de week werken.

	2 dagen werken	1 dag werken
Master in september	0.11	0.29
Geen master in september	0.66	0.54

Beschouw de gebeurtenissen

A1: Master in september
A2: Geen Master in September
B1: 2 dagen werken
B2: 1 dag werken

Nu kan men het volgende berekenen:

Ρ(Α1)=Ρ(Α1 ∩ Β1) + Ρ(Α1 ∩ Β2)=0,11 + 0,29=0,40

Ρ(Β1)=Ρ(Α1 ∩ Β1) + Ρ(Α2 ∩ Β1)=0,11 + 0,06=0,17

Als men nu probeert de kans van de vereniging van A1 en B1 te berekenen door middel van optelling van de kans op A1 en B1, vindt men

Ρ(Α1) + Ρ(Β1)=0,11 + 0,29 + 0,11 + 0,06

Let op dat hier twee keer Ρ(Α1∩Β1) optellen (0,11). Om deze dubbele optelling te corrigeren haalt men een keer Ρ(Α1∩Β1) van de som af, oftewel:

Ρ(Α1∪Β1)=Ρ(Α1) + (Ρ(Β1) - Ρ(Α1∩Β1)
Ρ(Α1∪Β1)=[0,11 + 0,29] + [0,11 + 0,06] - 0,11
Ρ(Α1∪Β1)=0,40 + 0,17 - 0,11=0,46

In geval van 3 willekeurige gebeurtenissen wordt automatisch de somregel ook langer:

P (A ∪ B ∪ C)= P (A) + P (B) + P (C) - P (A ∩ B) - P (A ∩ C) - P (B ∩ C) + P ∩ (A ∩ B ∩ C)

1.5 Theorema van Bayes

Voorwaardelijke kansen worden vaak gebruikt om relaties tussen twee gebeurtenissen te peilen. I voorbeeld 1c werd al aangegeven dat een voorwaardelijke kans de kans meet dat een gebeurtenis plaatsvindt, gegeven dat een mogelijke oorzaak van deze gebeurtenis al heeft plaatsgevonden. Al de kans op een gebeurtenis bekend is, maar de kans op een van de mogelijke oorzaken berekend dient te worden, kunnen problemen ontstaan. Het theorema van Bayes biedt hiervoor de oplossin Hieronder zal alleen de formule van het theorema van Bayes gegeven worden, daar er in de studieboeken van de Bedrijfsstatistiek hier maar kort op ingegaan wordt.

Theorema van Bayes:

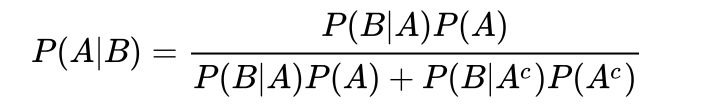
Voor meer achtergrondinformatie over het theorema van Bayes dient de lezer er geavanceerde statistiekboeken op na te slaan.

1.6 Combinatoriek of combinatieleer

In de combinatoriek of combinatieleer bestudeert men eindige verzamelingen van objecten die aan gespecificeerde eigenschappen voldoen. In het bijzonder houdt men zich bezig met het "tellen" van objecten in deze verzamelingen en het bepalen of er zekere "optimale" objecten in een verzameling aanwezig zijn1.

Binnen de combinatoriek kent men 4 "hoofdcategorieën". Hieronder worden deze categorieën zo overzichtelijk mogelijk uiteengezet met de corresponderende formules.

1.6.1 Herhalingsvariatie

Men kiest k elementen uit n; hier is de volgorde van belang en er sprake van trekken met terugleggen. De formule die men hiervoor hanteert is

N k

1.6.3 Combinatie

Men trekt k elementen uit een verzameling n; hier is de volgorde niet van belang en er is sprake van trekken zonder terugleggen. De formule die men hiervoor hanteert is

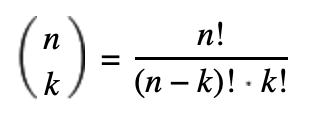
1.6.4 Herhalingscombinatie

Men trekt k elementen uit een verzameling n ; hier is de volgorde niet van belang en er is sprake van trekken met terugleggen. De formule die men hiervoor hanteert is

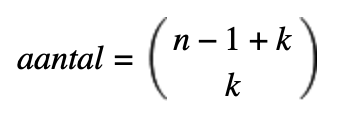
2. Populaties, steekproeven, stochastische variabelen en kansverdeling

2.1 Populaties en de aselecte steekproef

In de statistiek is een populatie een ten aanzien van bepaalde aspecten homogene verzameling van objecten waarop het onderzoek zich richt2. Als voorbeeld in dit hoofdstuk zullen in dit hoofdstuk schroeven worden genomen. De populatie bestaat dan uit het aantal schroeven dat een fabriek per kwartaal produceert. Ieder kwartaal zal de machine die de schroeven produceert opnieuw worden afgesteld om zo de gemiddelde, standaard lengte van iedere geproduceerde schroef te waarborgen. Als men de gemiddelde lengte van de schroeven wil onderzoeken gaat men uiteraard niet iedere schroef individueel onderzoeken. Dit zou immers veel te veel tijd kosten. In plaats daarvan doet men een steekproef en dit is tevens de term voor het aantal te onderzoeken schroeven. Belangrijk hierbij is dat deze steekproef aselect is en dat houdt in dat iedere schroef die in een kwartaal wordt geproduceerd evenveel kans heeft om in de steekproef terecht te komen. Als gevolg zal iedere steekproef andere resultaten opleveren en door middel van de kansrekening kan men hier uitspraken over doen. (Let op! Uitspraken zijn geen conclusies!)

2.2 De stochastische variabele

De formele definitie van een stochastische variabele X is een (meetbare) reële functie in de uitkomstenruimte Ω 3. In het geval van de schroeven dat hierboven is beschreven zou men uit de uitkomstenruimte=Ω {alle in een kwartaal geproduceerde schroeven} de volgende stochastische variabele kunnen afleiden:

X ="Lengte, afgerond in millimeters, van een schroef "

Voor de stochastische variabele worden meestal hoofdletters gebruikt zoals X, Y en Z. Sommige statistische literatuur hanteert kleinere, onderstreepte letters zoals x, y en z.

2.3 Kansverdeling

Een kansverdeling is een tabel, formule of grafiek die de waarden van een stochastische variabele en de kans corresponderend met deze waarden beschrijft. Deze kansverdeling is van belang voor de statistische analyse die men wil uitvoeren en de kansverdeling wordt opgevat als een model voor de werkelijke verdeling, daar de werkelijke verdeling immers onbekend is. Het is de bedoeling van de statistische analyse om uitspraken te doen over de parameter(s) die de theoretische kansverdeling bepalen. Er bestaan verschillende vormen van uitspraken over parameters. Het kan (1) een schatting van een parameter betreffen, (2) gaan om het toetsen van een hypothese over een parameter of (3) het bepalen van een betrouwbaarheidsinterval voor de parameter.

2.4 Discrete en continue kansverdeling

Als een stochastische variabele discreet is, houdt dat in dat deze variabele een telbaar aantal uitkomsten kan hebben. Wanneer er bijvoorbeeld wordt gekeken hoe vaak men "kop" werpt als men 10 keer een euromunt opgooit, zijn de waarden van de stochastische variabele X ₀, ₁, ₂, ..., ₁₀. X kan in totaal 11 verschillende waarden aannemen. De kansverdeling van een discrete stochastische variabele die waarden kan aannemen uit de verzameling K, wordt volledig bepaald door de kansen p(k)= P(X = k)

Nu kunnen er twee vereisten voor discrete stochastische variabelen vastgesteld worden:

1. 0 ≤ p (k_i) ≤ 1 _{voor alle ki}
2. ∑ _k ∈ K p(k)=1 _{(dit heet ook wel de kansfunctie)}

Voorbeeld 2a

Stephanie werkt bij een callcenter en heeft ingepland dat ze morgen 3 mensen gaat bellen. Ze weet uit ervaring dat de kans dat ze een klant binnenhaalt 20% per gesprek is. Geef de kansverdeling voor het aantal klanten dat morgen binnengehaald wordt. (Hint: maak eerst een kansboom)

Na het maken van een kansboom en het vaststellen van X="aantal binnengehaalde klanten" kan men concluderen dat:

p(0)=0,512
p(1)=0,128 + 0,128 + 0,128=0,384
p(2)=0,032 + 0,032 + 0,032=0,096
p(3)=0,008

Als een stochastische variabele continu is, houdt dat in dat deze variabele niet telbaar is. Met andere woorden, de mogelijke waarden voor de variabele is oneindig. Een goed voorbeeld hiervan is de tijd die nodig is om een taak te voltooien. Bijvoorbeeld X ="de tijd nodig om een tentamen te maken op de Universiteit waar 3 uur voor staat en studenten mogen pas na 1 uur weg". De kleinste waarde die X kan hebben is 60 (minuten). De grootste waarde voor X is 180. Tussen 60 en 180 kan X oneindig veel waarden hebben. Een student kan bijvoorbeeld na 60,1 minuten weg gaan, maar ook na 60,01 minuten. Of na 60,001 minuten of na 103,04245 minuten. Kortom, X heeft oneindig veel mogelijkheden en is daarom een continue stochastische variabele.

Indien meer dan 1 variabele een rol spelen, is er sprake van een zogenaamde stochastische vector. De stochastische vector is de combinatie van de stochastische variabelen, oftewel

X =( X₁,..., X_k )

3. Verwachtingswaarde, variantie, standaard deviatie en covariantie

Het populatiegemiddelde geeft het gewogen gemiddelde aan van alle waarden in een populatie. De variantie geeft de spreiding aan van de waarden binnen de populatie. Hieronder zijn de formules voor beide termen te vinden:

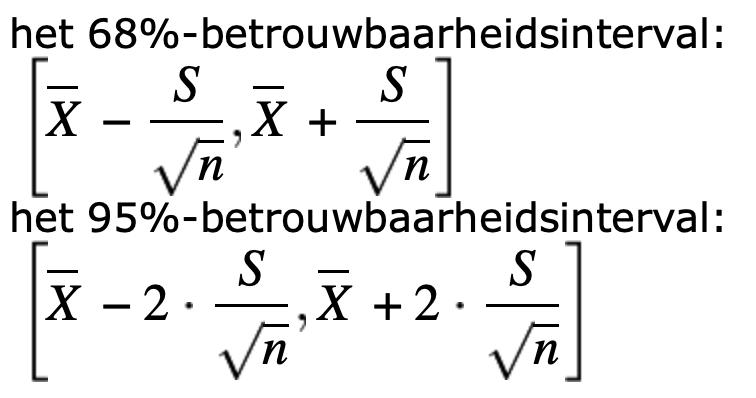
4 Chebyshev en de centrale limietstelling

4.1 Theorema van Chebyshev

Voordat men het theorema van Chebyshev kan uitleggen moet men bekend zijn met een aantal regels omtrent de relatie tussen het gemiddelde en de standaarddeviatie. Er zijn drie regels die gelden wanneer een vorm van het histogram een bel betreft:

1. Ongeveer 68% van alle waarden valt binnen 1 standaarddeviatie van het gemiddelde.
2. Ongeveer 95% van alle waarden valt binnen 2 standaarddeviaties van het gemiddelde.
3. Ongeveer 99,7% van alle waarden valt binnen 3 standaarddeviaties van het gemiddelde.

Als men het bovenstaande beschouwd kan men een meer algemene interpretatie van de standaarddeviatie toepassen, te weten het theorema van Chebyshev:

Als k bijvoorbeeld 3 is, dan is volgens het theorema van Chebyshev tenminste 89%  van de waarden binnen 3 standaarddeviaties van het gemiddelde liggen. Dit theorema is toepasbaar op iedere soort kansverdeling.

4.2 Theorema van de centrale limietstelling

Het theorema van de centrale limietstelling is een van de belangrijkste begrippen uit de statistiek. Deze geeft aan dat de som van een groot aantal onderling onafhankelijke en gelijk verdeelde stochastische variabelen met eindige variantie bij benadering een normale verdeling heeft. Hoe groter dit aantal, hoe dichter de verdeling bij een normale verdeling licht.

5. Beschrijvende statistiek

5.1 Categorieën variabelen

In de statistiek onderscheidt men 4 hoofdgroepen variabelen: Nominaal, ordinaal, interval en ratio. De verschillen tussen deze 4 categorieën zijn redelijk eenvoudig aan te geven. Als men bijvoorbeeld kijkt naar een hardloopwedstrijd met verschillende deelnemers, dan is een nummer van een renner een nominale variabele. Dit nummer heeft geen waarde en wordt alleen gebruikt voor het identificeren van individuele renners. Een ordinale variabele zou kunnen zijn de volgorde waarop de renners over de eindstreep binnenkomen, bijvoorbeeld als eerste, tweede, zesde, veertigste, enz. Hier heeft het getal weldegelijk een waarde, want het zegt iets over de volgorde van renners. Een interval variabele met betrekking tot de renners zou kunnen zijn dat de renners beoordeeld worden op een schaal van 0 tot 10, waar 0 heel slecht is en 10 heel goed. De ratio variabele kan bijvoorbeeld de tijd zijn waarin de renners de wedstrijd uitlopen en kan iedere waarde aannemen.

Naast categorieën variabelen heeft men ook een aantal maten nodig in de statistiek. Men onderscheidt respectievelijk locatiematen, spreidingsmaten en maten voor een lineaire samenhang.

5.2 Locatiematen

Locatiematen geven informatie over de locatie van het centrum van de verdeling. De belangrijkste locatiematen binnen de beschrijvende statistiek zijn modus, mediaan en gemiddelde. De modus wordt gedefinieerd als de waarde (of waarden) die het meeste voorkomt. De mediaan wordt berekend door alle waarden op volgorde te zetten (van laag naar hoog of van hoog naar laag). De waarde in het midden is de mediaan. Het gemiddelde wordt simpelweg berekend door de waarden bij elkaar op te tellen en te delen door het aantal waarden.

5.3 Spreidingsmaten

Deze maten hebben als doel om aan te geven in welke mate de waarden van een verdeling of steekproef uiteenlopen en zijn alleen van toepassing op kwantitatieve interval en ratio variabelen. De meest gebruikte spreidingsmaten zijn het bereik, de standaarddeviatie en de variatiecoëfficiënt. Het bereik is niets anders dan het verschil tussen de grootste waarde en de kleinste waarde. Soms is het bereik oneindig en dus onbruikbaar.

5.4 Maten voor lineaire samenhang

In §3.3 zijn de begrippen covariantie en correlatiecoëfficiënt al besproken. In deze paragraaf worden de covariantie en correlatiecoëfficiënt met betrekking tot steekproeven behandelt (de zogenaamde steekproefcovariantie  en steekproefcorrelatiecoëfficiënt  ).

6. Het toetsen van hypotheses

Het doel van het toetsen van hypotheses is het vaststellen of er voldoende statistisch bewijs is om te concluderen dat een bewering of hypothese over een parameter ondersteund wordt door de data. Het toetsen van hypotheses vormt een basis in de statistiek en is de fundering van menig statistisch onderzoek.

6.1 H0 en H1

Aan de hand van een voorbeeld zullen de termen H₀ en H₁ toegelicht worden. Stel iemand wordt beschuldigd van het begaan van een overtreding. Dan kunnen twee zaken e geval zijn. De verdachte is schuldig of de verdachte is niet schuldig. In de statistiek giet men dit in een hypothese vorm waarbij H₀ de nulhypothese wordt genoemd en H₁ de alternatieve hypothese wordt genoemd. Kortom:

H₀: de verdachte is onschuldig

H₁: de verdachte is schuldig

Natuurlijk weet men van tevoren niet of de verdachte wel of niet schuldig is. Bewijs zal moeten aantonen wat het geval is. Er zijn twee mogelijke beslissingen. De verdachte veroordelen of de verdachte vrijspreken. In statistisch jargon is het veroordelen van de verdachte gelijk aan het verwerpen van de nulhypothese ten gunste van het alternatief. Het vrijspreken van de verdachte staat voor het niet verwerpen van de nulhypothese ten gunste van het alternatief.

6.2 Fouten van de eerste en tweede soort

Bij het testen van hypotheses zijn er twee mogelijke fouten die kunnen voorkomen. Er is sprake van een fout van de eerste soort indien een nulhypothese wordt verworpen die eigenlijk waar is. Een fout van de tweede soort houdt in dat een foutieve nulhypothese niet verworpen wordt.

In het voorbeeld hierboven zou sprake zijn van een fout van de eerste soort indien een onschuldig persoon veroordeeld zou worden. Een fout van de tweede soort zou zich voordoen als een schuldig persoon zou worden vrijgesproken.
De kans op een fout van de eerste soort noteert men als aen dit noemt men ook wel het significantie niveau. De kans op een fout van de tweede soort noteert men als β. De kansen op fouten α en β zijn aan elkaar gerelateerd wat inhoudt dat elke poging om de een te verlagen de ander automatisch verhoogt.

6.3 Soorten alternatieve hypotheses

Natuurlijk wil men onderzoek ook andere zaken onderzoeken dan puur een nulhypothese die synoniem staat voor "het is zo" en een alternatieve hypothese die synoniem staat voor "het is niet zo". In het voorbeeld hierboven is hier sprake van. Als men echter onderzoek wil verrichten naar de lengte van schroeven die een machine produceert zou men, indien een schroef een gemiddelde lengte van 50 mm zou moeten hebben, de volgende nulhypothese en alternatieve hypothese kunnen opstellen:

H₀: μ=50

H₁: μ ≠ 50

Wat nu opvalt is dat, indien de nulhypothese wordt verworpen, de schroeven óf groter zijn dan 50 mm, of kleiner zijn dan 50 mm. Dit noemt men een tweezijdige hypothese.

Indien men wil onderzoeken of de schroeven groter zijn dan 50 mm dan wordt de alternatieve hypothese:

H₁: μ > 50

Dit noemt men een (rechts)eenzijdige hypothese.

Indien men wil onderzoeken of de schroeven groter zijn dan 50 mm dan wordt de alternatieve hypothese:

H₁: μ < 50

Dit noemt men een (links)eenzijdige hypothese.

6.4 Kritieke gebied

Bij het testen van hypotheses wordt altijd bepaalt welke toetsingsgrootheid wordt getest. De waarde van deze toetsinggrootheid speelt een rol bij het wel of niet verwerpen van de nulhypothese. Overschrijden deze waarden de waarden die van tevoren vastgesteld zijn om de nulhypothese te verwerpen dan wordt de nulhypothese verworpen. Dit kritieke gebied is zo'n gebied van waarden dat als de toetsingsgrootheid in dat gebied valt, de nulhypothese wordt verworpen.

De zogenaamde p-waarde speelt hier ook een rol. In het algemeen geldt dat als de p-waarde kleiner is dan de a(fout van de eerste soort) dat de nulhypothese wordt verworpen.

6.5 7 stappen schema

Er bestaat een schema bestaande uit 7 stappen dat het testen van hypotheses overzichtelijk maakt. Hieronder wordt het 7 stappen schema van de zogenaamde klassieke methode besproken:

1. Stel H₀ en H₁ vast
2. Stel de toetsingsgrootheid vast
3. Stel de kritieke waarden vast → verwerpt men H₀ voor grote waarden, kleine waarden of voor zowel grote als kleine waarden?
4. Stel het significantieniveau avast
5. Bepaal het kritieke gebied door middel van het opzoeken van de kritieke waarden van de test
6. Bereken de toetsingsgrootheid → valt deze binnen het kritieke gebied, dan wordt H₀ verworpen op significantie niveau a. Is dit niet het geval, dan wordt H0 niet verworpen op significantieniveau a.
7. Geef een duidelijke conclusie voor een breed publiek.

Naast de klassieke methode kan ook de p-waarde methode gehanteerd worden. Hier zijn stap 1 tot en met 4 hetzelfde als bij de klassieke methode:

1. Stel H₀ en H₁ vast
2. Stel de toetsingsgrootheid vast
3. Stel de kritieke waarden vast → verwerpt men H₀ voor grote waarden, kleine waarden of voor zowel grote als kleine waarden?
4. Stel het significantieniveau avast
5. Bereken de toetsingsgrootheid
6. Stel de p-waarde vast → Als p-waarde ≥ α dan wordt H₀ verworpen op significantie niveau α. Is dit niet het geval, dan wordt H₀ niet verworpen op significantieniveau α
7. Geef een duidelijke conclusie voor een breed publiek

7. Binomiaal verdelingen

Binomiale verdelingen zijn het resultaat van zogenaamde binomiale experimenten. Binomiale experimenten hebben de volgende eigenschappen:

1. Een binomiaal experiment bestaat uit een vast aantal pogingen. Het aantal pogingen wordt genoteerd alsn.
2. Elke keer zijn er 2 mogelijke uitkomsten. De ene uitkomst noemt men success, dan andere uitkomst failure.
3. De kans op success is p. De kans op failure is 1-p.
4. De pogingen zijn onafhankelijk wat inhoudt dat de uitkomst van een keer geen invloed heeft op andere pogingen.

De stochastische variabele staat voor het aantal keren success in n pogingen. Deze variabele noemt men ook wel de binomiale stochastische variabele.

Een kort voorbeeld:

Quirine gooit 10 keer met een 1 euromunt. Het aantal pogingen n is dus 10. Quirine wil zo vaak mogelijk "kop"gooien, dus ze beschouwt "kop" gooien als success. Als er sprake is van een zuivere munt, dan is de kans op "kop" 50%, dus p=0,5. Ook kan er geconstateerd worden dat de pogingen onafhankelijk zijn, daar een worp met de munt geen invloed heeft op een vorige of volgende worp.

7.1 Binomiale stochastische variabele

Zoals al eerder vermeld is de binomiale stochastische variabele het aantal keren success in n pogingen van het experiment. Deze variabele kan waarden aannemen als 0, 1, 2, ..., n, kortom de stochastische variabele is discreet. Men moet in staat kunnen zijn te berekenen welke kans gerelateerd is aan elke waarde.

Als men een kansboom maakt met bij iedere fase twee takken (uitkomsten) die staan voor success en failure, is het duidelijk dat om de kans te berekenen op x keer success met n pogingen er voor elke success in de reeks vermenigvuldigd dient te worden met p. Als er x keren success zijn dan zijn er dus ook n-x keren failure. Elke failure in de reeks dient vermenigvuldigd te worden met 1-p. Kortom, de de kans voor elke reeks takken (in de kansboom) de staan voor x keer succes en n-x keer failure.

In een kansboom kunnen combinaties zich op verschillende manieren voordoen. Met een munt is bijvoorbeeld de combinatie "kop en munt" mogelijk als "kop-munt" of "munt-kop". Met de onderstaande formule kan men het aantal takkenreeksen berekenen met x keer success en n-x keer failure:

8. Poisson verdeling

Een andere handige discrete kansverdeling is de Poisson verdeling. De Poisson stochastische variabele geeft het aantal gevallen van gebeurtenissen weer, die hier ook weer aantal keren success noemen. Het grote verschil met de binomiale verdeling is dat er bij de Poisson verdeling geen sprake is van een vast aantal pogingen. Bij de Poisson verdeling gaat het om het aantal keren success in een bepaald tijdsinterval of specifieke plaats. Een voorbeeld hiervan is het aantal, dagelijkse ongelukken op een specifiek stuk snelweg. Het Poisson experiment heeft de volgende eigenschappen:

Het aantal keren success dat plaatsvindt in elk willekeurig interval is onafhankelijk van het aantal keren success in elk ander willekeurig interval

1. de kans op success in een interval is even groot in intervallen van dezelfde grootte
2. de kans op success is evenredig aan de grootte van het interval
3. de kans op meer dan 1 success in een interval ligt dichter bij 0 naarmate het interval kleiner wordt

Als algemene regel geldt dat een Poisson stochastische variabele staat voor het aantal keren dat een relatief zeldzame gebeurtenis die willekeurig en onafhankelijk plaatsvindt. Bijvoorbeeld het aantal mensen dat bij een restaurant binnenkomen is geen Poisson verdeling, want mensen komen meestal in groepen naar een restaurant en dat is in strijd met de eerste eigenschap van het Poisson experiment, te weten het ontbreken van onafhankelijkheid.

De formule voor de Poisson kansverdeling:
Als X een Poisson stochastische variabele is, dan is de kans dat deze een waarde aanneemt van x.

waar µ het gemiddelde aantal keren success is in het bepaalde interval of de specifieke plaats en e is de basis van het natuurlijke algoritme (ongeveer 2,71828).

9. Continue kansverdelingen

9.1 Uniforme kansverdeling

De eerste continue kansverdeling die hier besproken zal worden is de uniforme kansverdeling. Vergeleken andere kansverdelingen is de praktische toepassing van de uniforme verdeling beperkt.

De uniforme verdeling wordt beschreven door de functie

De uniforme verdeling wordt ook wel rechthoekige verdeling genoemd vanwege de rechthoekige vorm van de kansdichtheidsfunctie f (x).

Om de kans van elk willekeurig interval te berekenen, kijkt men naar het gebied onder de curve. Wil men bijvoorbeeld de kans berekenen dat X tussen x₁ en x₂ valt, dan kijkt men naar het gebied met als basis x₂-x₁ en als hoogte 1/(b-a).

9.2 Normale verdeling

De normale verdeling is de belangrijkste van de kans verdelingen door de cruciale rol die deze vervult in het universum van de statistiek.

De kansdichtheidsfunctie van een normaal verdeelde variabele is

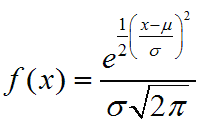
Hier is e=2,71828 en π=3,14159

De onderstaande figuur geeft een normale verdeling weer. Wat opvalt is dat de curve symmetrisch is door het midden (gemiddelde μ) en de verdeelde variabele ligt tussen -∞ en ∞.

Bij de normale verdeling spelen twee parameters een grote rol, het gemiddelde μ en de standaarddeviatie s. Als μ groter wordt, verschuift de gehele curve naar rechts en als μ kleiner wordt, verschuift de curve naar links.

Bij de standaarddeviatie gebeurt iets anders bij het vergroten en verkleiner. Als sgroter wordt, naar de breedte van de curve toe en als skleiner wordt, zal de breedte van de curve afnemen.

9.3 Het berekenen van normale kansverdelingen

Om de kans te berekenen dat een normaal verdeelde variabele in een bepaald interval valt, dient men het gebied in het interval onder de curve te berekenen. Helaas is de formule hiervoor niet zo eenvoudig als voor de uniforme verdeling. Bij deze berekening is een tabel van toepassing waar de normaal verdeelde variabele in gestandaardiseerd is.

Standaardiseren gebeurt door middel van door het gemiddelde μ van de normaal verdeelde variabele X af te trekken en deze uitkomst te delen door de standaarddeviatie s. De noemt men de standaard normaal verdeelde variabele Z.

Aan de hand van een voorbeeld wordt hieronder uitgelegd hoe de tabel in Appendix A1 te gebruiken. (dit voorbeeld is erg belangrijk en bevat ook uitleg!)

9.4 Waarden van z vinden

In enkele gevallen is het nodig om de waarde van z vast te stellen gegeven een bepaalde kans. Hier wordt de notatie zA gebruikt om de waarde van z aan te geven op zo'n wijze dat het gebied aan de rechterkant hiervan onder de standaard normale curve A is. Oftewel, z_A is een waarde van een standaard normaal verdeelde variabele op zo'n wijze dat

Om z_A voor elke willekeurige waarde van A vinden dient de tabel van de normale kansverdeling omgekeerd gebruikt te worden. Om dit te kunnen doen moet men een kans specificeren en de corresponderende z-waarde vaststellen. Bijvoorbeeld de waarde z_0.025. Door het format van de tabel (standaard normaal) moet men eerst het gebied tussen 0 en z_0.025 vaststellen. Dit is gelijk aan . (aangegeven in 4 decimalen, daar de waarden in de tabel tevens in 4 decimalen weergegeven zijn). Ze z-waarde uit de tabel corresponderend met een kans van 0,4750 is 1,96. Met andere woorden, z_0.025 =1,96 en dat houdt in dat P(Z > 1,96)=0,025.